A* 알고리즘의 이해
A* 알고리즘은 다익스트라 알고리즘과 최선 우선 탐색의 장점을 적절히 결합한 알고리즘입니다.
흔히 게임에서 플레이어를 쫓는 적 캐릭터에 해당 알고리즘을 적용하는 것으로 알려져 있습니다.
이 알고리즘을 왜 사용하고, 어떻게 사용해야 하는지에 대해서 간단하게 다루어보겠습니다.
A* algorithm
A* 알고리즘은 출발 지점에서 목표 지점까지의 최단거리를 구하는 알고리즘입니다.
다익스트라는 출발 지점으로부터 다른 모든 지점의 최단거리를 각각 구했다면, A*는 다익스트라에 비교했을 때
불필요한 최단거리는 구하지 않는 것이 특징이라고 할 수 있습니다.
어떻게 각각의 경로가 필요한 최단거리인지, 불필요한 최단경로인지 알 수 있을까요?
바로 다음 두 가지를 고려하는 것입니다.
- 시작부터 이미 이동한 거리
- 목표까지 남은 거리에 대한 추정값
A* 알고리즘은 위 정보의 조합으로 다음에 어떤 경로를 탐색할지에 대한 정보에 입각한 결정을 내릴 수 있습니다.
예시
다음 예시를 통해 살펴봅시다.
6개의 정점을 가진 그래프에서 0번 정점을 출발 지점, 5번 지점을 목표 지점이라고 했을 때,
최단 경로를 구해보겠습니다.
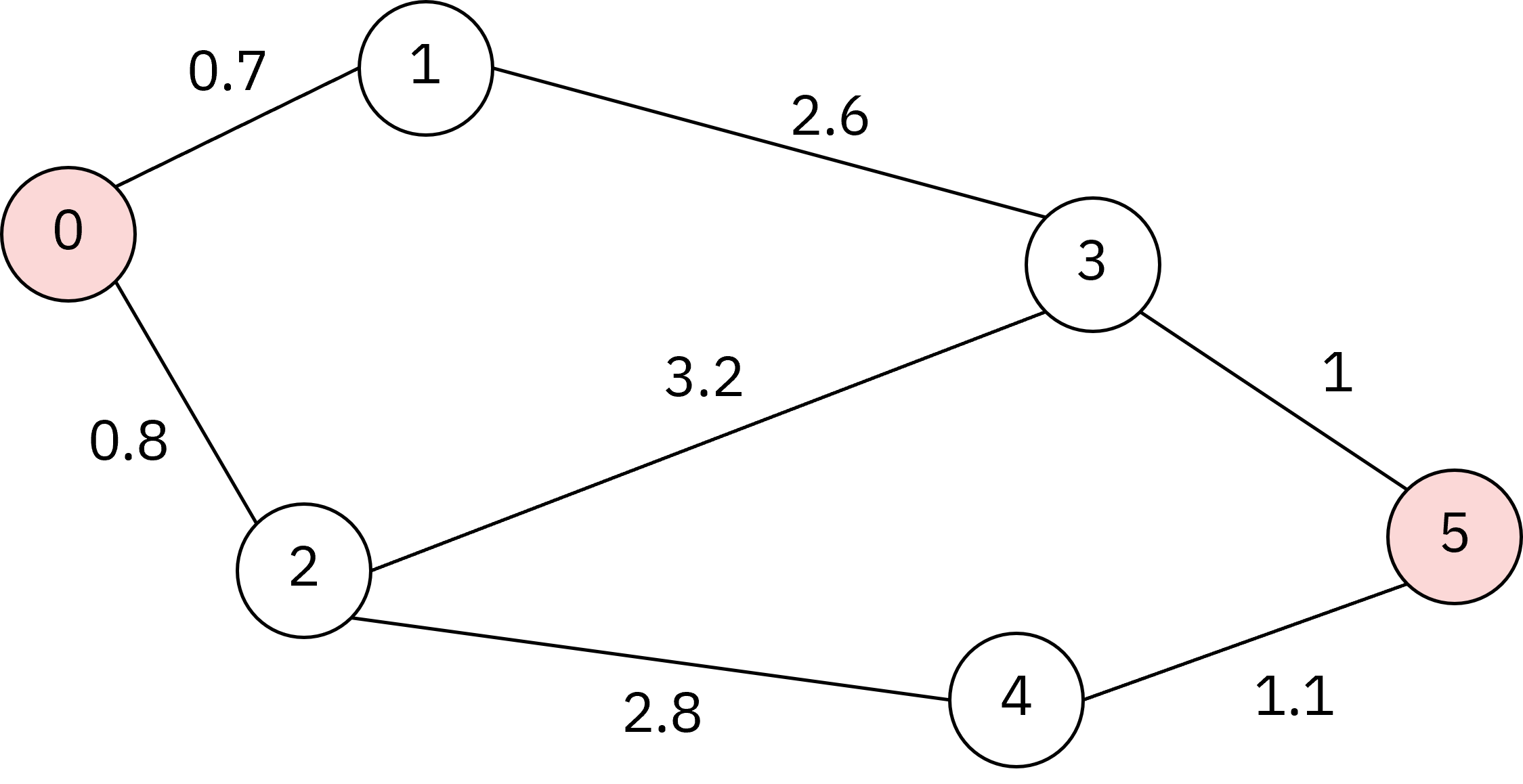
(다음 예시 설명은 해당 글을 기반으로 작성되었으므로, 자세한 내용은 여기서 참고하시길 바랍니다.)
A* 알고리즘을 통한 최단 경로 탐색을 위해 가장 먼저 수행하는 첫 과정은 다음과 같습니다.
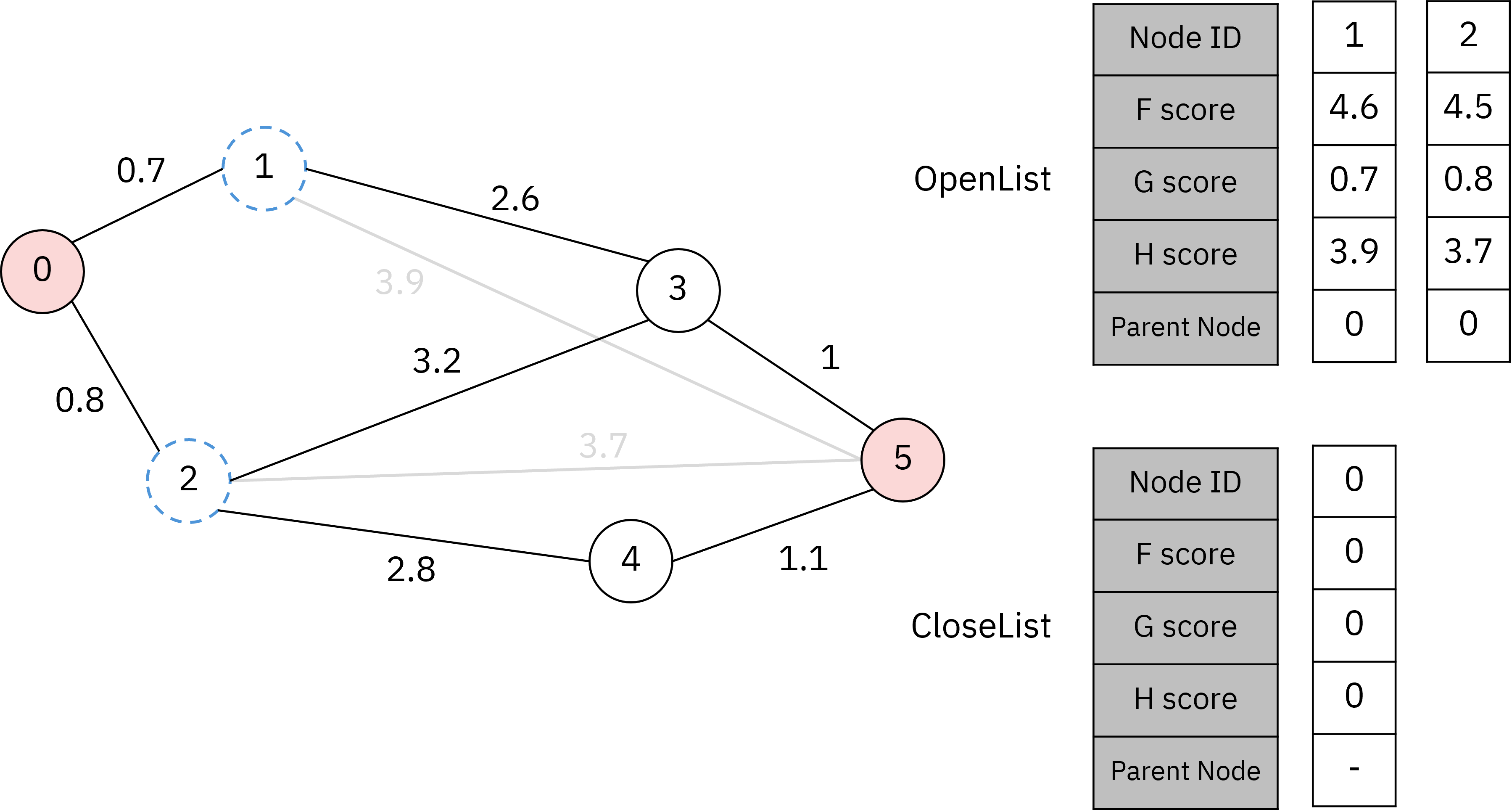
A* 에서는 OpenList와 CloseList 두 저장소를 사용하여 최단 경로 분석을 진행합니다.
위 그림에서 OpenList는 최단 경로를 분석하기 위한 상태값들을 계속 갱신하며, CloseList는 처리가 완료된 정점을 담아 두기 위해 사용합니다.
그림 속 표에서 F score는 총 예상 가중치(비용), G score는 출발 노드로부터 해당 노드까지의 실제 가중치, H score는 해당 노드로부터 도착 노드까지의 예상 가중치 입니다.
또한 F = G + H 입니다.
먼저 출발 노드인 0을 CloseList에 추가하고 연결된 노드인 1, 2번 노드를 OpenList에 추가합니다.
H score는 단순히 해당 노드로부터 도착 노드까지의 유클리드 거리를 사용해서 구한다고 가정합시다.
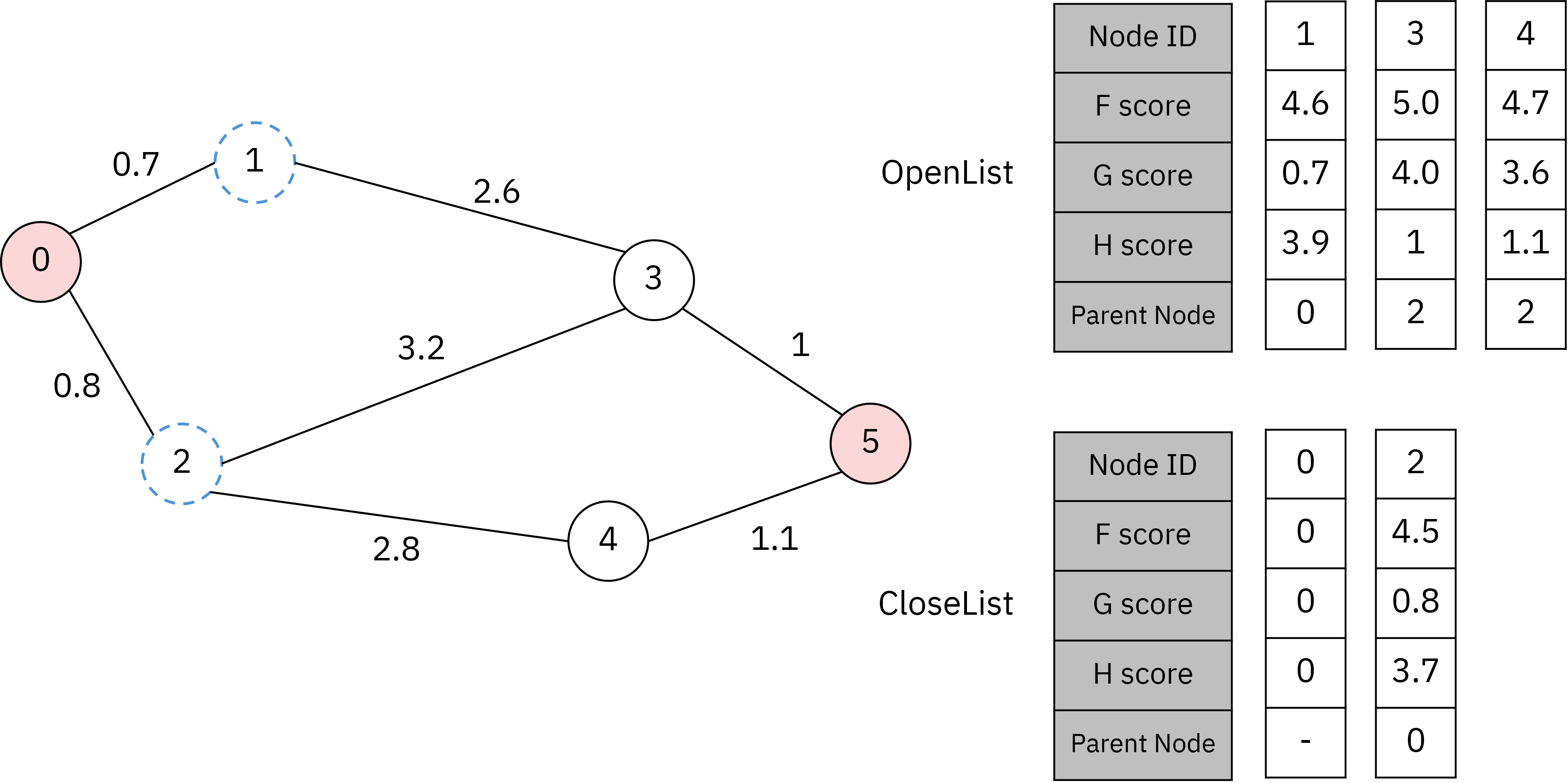
다음 단계는 OpenList에서 가장 작은 F score를 가지는 노드 하나를 CloseList에 옮기는 과정입니다.
위 그림에서는 2번 노드가 들어가게 됩니다.
그리고 CloseList에 들어간 2번 노드에 연결된 노드인 3, 4번 노드를 OpenList에 추가합니다.
이 때 3, 4번 노드는 현재 부모 노드인 2번 노드에 연결된 경로로 G score가 정해집니다.
(단, 3, 4번의 H score는 실제 경로의 가중치와 같다고 가정합니다.)
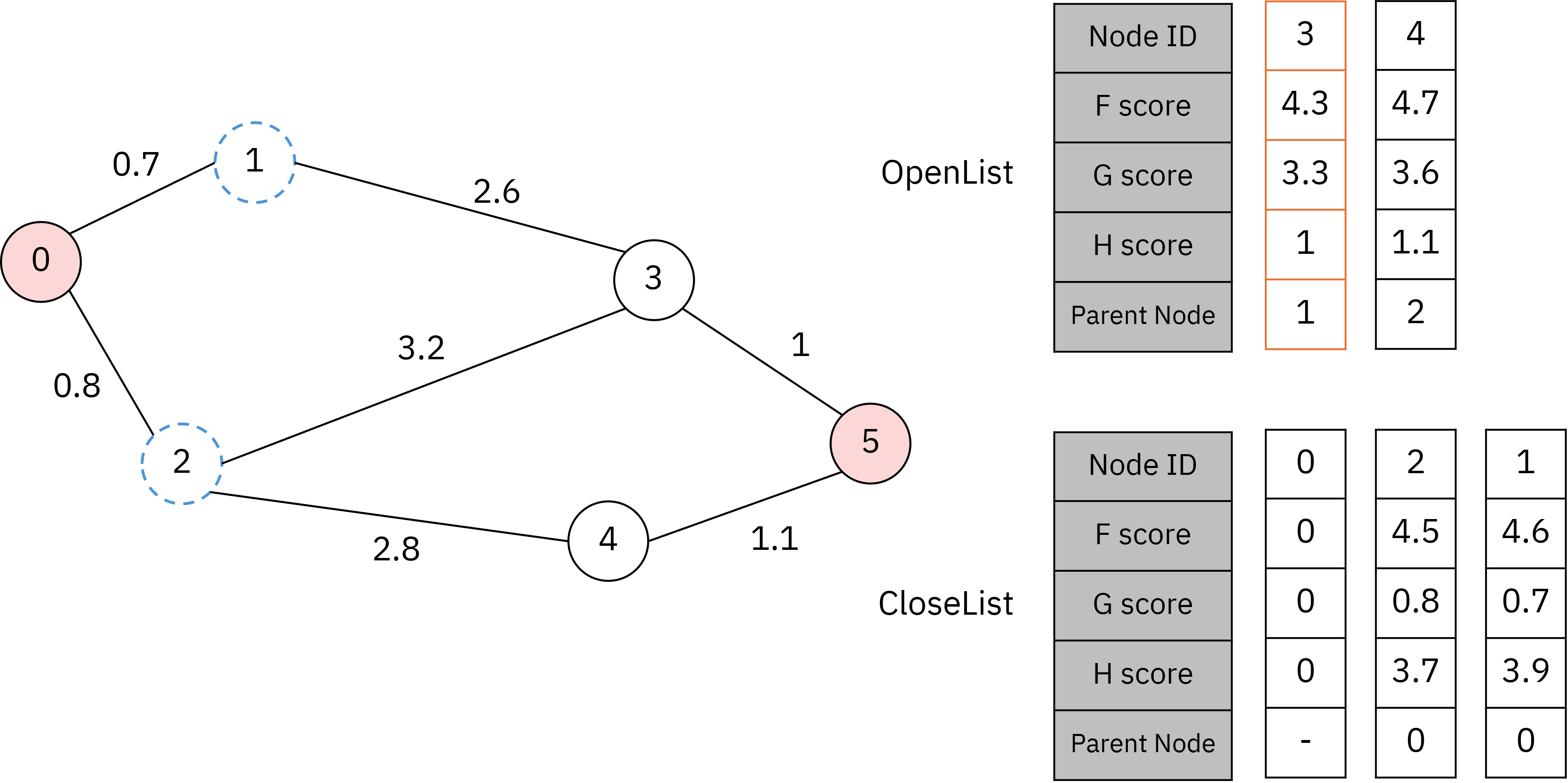
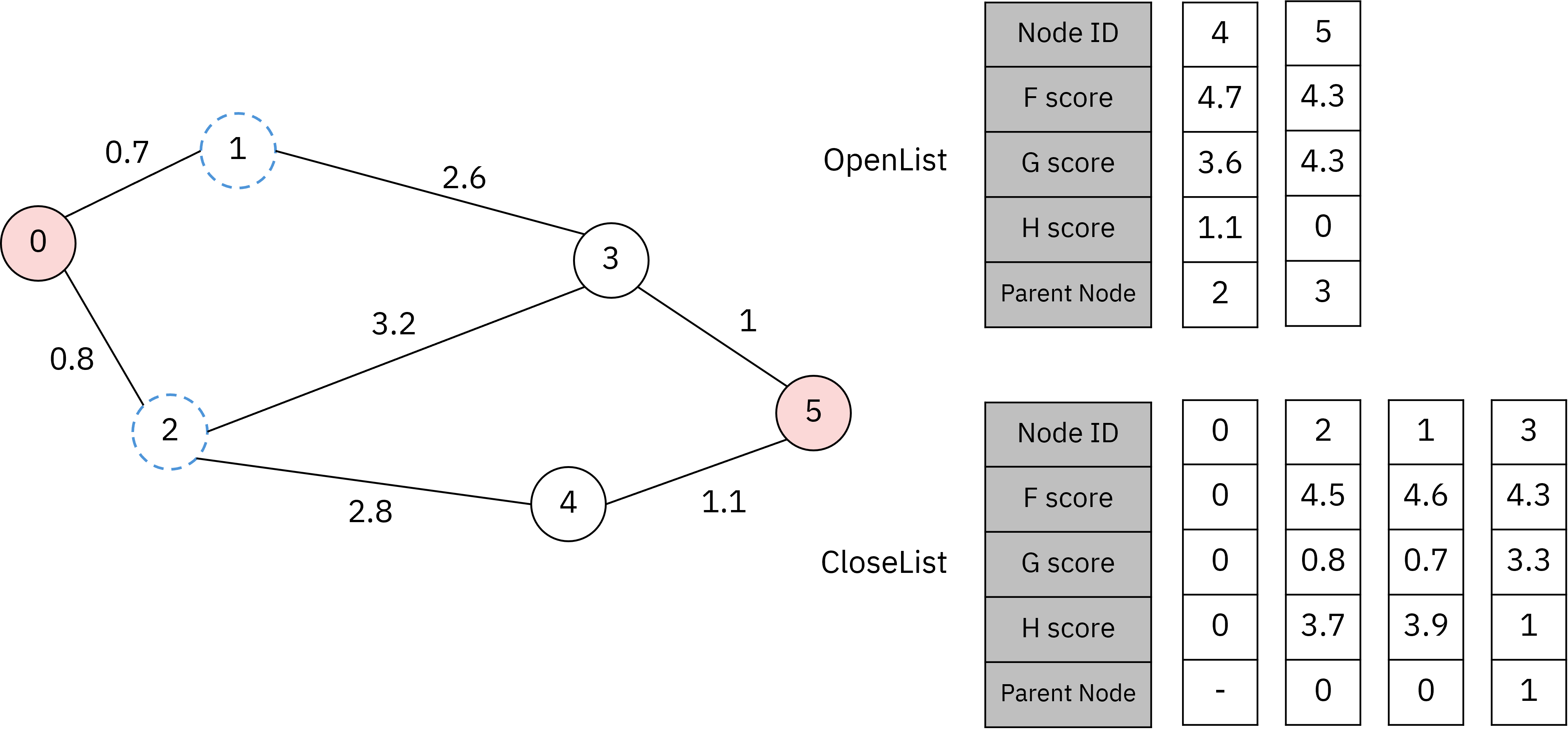
다음 단계부터는 비슷한 작업의 반복 과정입니다.
OpenList에서 가장 작은 F score를 가지는 노드를 CloseList에 추가하고,
CloseList에 추가된 노드와 연결된 노드를 OpenList에 추가, 혹은 갱신합니다.
위 그림에서 주의 깊게 볼 점은 1번 노드가 CloseList에 추가됨으로써 3번 노드의 상태값이 갱신되었다는 점입니다. 이처럼 다른 부모 노드에 의해 최솟값이 갱신되는 경우가 발생할 수 있습니다.
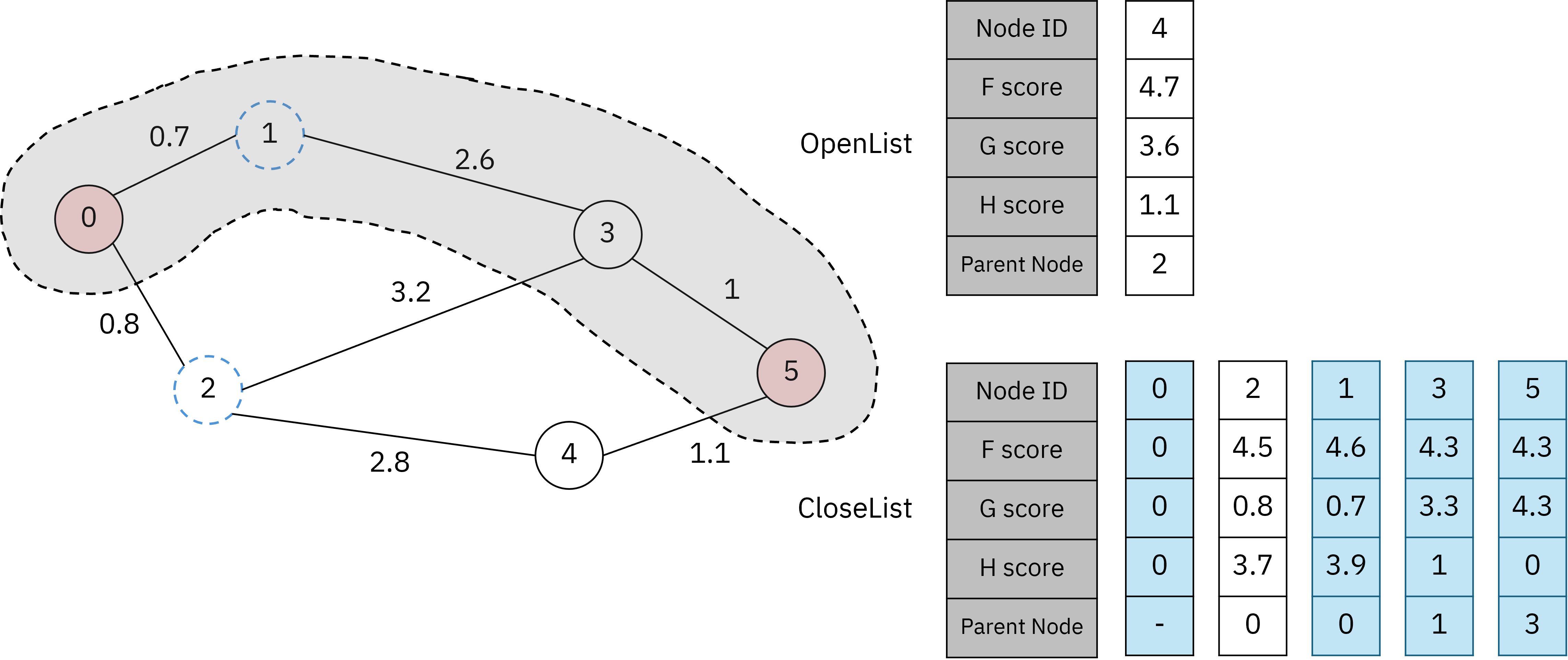
이후 두 단계가 지나면 도착 노드가 CloseList에 추가됩니다.
도착 노드가 CloseList에 추가된 순간 A* 알고리즘은 종료됩니다.
우리는 이제 CloseList를 토대로 최단경로를 파악할 수 있습니다.
위 그림 속 CloseList에서 5$\leftarrow$3$\leftarrow$1$\leftarrow$0 순으로 해당 노드의 부모 노드를 찾아가는 방식으로 최단 경로를 구할 수 있습니다.
비용 함수의 이해
A* 알고리즘은 앞서 설명한 두 가지 개념과, 그 두 개념을 합친 추정값을 사용하여 경로를 효율적으로 평가합니다.
\[\begin{flalign*} &f(n) = g(n) + h(n) & \end{flalign*}\]$g(n)$을 출발 지점에서 현재 지점까지의 비용,
$h(n)$을 현재 지점에서 목표 지점까지의 예상 비용이라고 했을 때
$f(n)$이 가장 작은 지점을 다음 지점으로 설정합니다.
경로 비용 $g(n)$
경로 비용 함수 $g(n)$은 탐색 과정에서 초기 시작 노드에서 현재 위치까지의 정확한 거리를 나타냅니다.
이 비용은 선택한 경로를 따라 이동한 모든 개별 간선 가중치를 더해 계산됩니다.
수학적으로, 노드 $n_0$(시작 노드)에서 $n_k$(현재 노드)까지의 경로에 대해 $g(n)$을 다음과 같이 표현할 수 있습니다.
\[\begin{flalign*} &g(n_k) = \sum_{i=0}^{k-1} w(n_i, n_{i+1}) & \end{flalign*}\]휴리스틱 함수 $h(n)$
휴리스틱 함수 h(n)은 현재 노드에서 목표 노드까지의 예상 비용을 제공하며, 이는 알고리즘이 남은 경로에 대해
“정보에 입각한 추측” 역할을 합니다. 휴리스틱에 대해서는 마지막에 추가로 다루도록 하겠습니다.
수학적으로, 주어진 노드 $n$에 대해 휴리스틱 추정치는 $h(n) \le h’(n)$ 조건을 만족해야 합니다. 여기서 $h’(n)$은 목표에 대한 실제 비용이므로 실제 비용을 과대평가하지 않으면 허용 가능합니다.
격자 기반 또는 지도 기반 문제에서 일반적인 휴리스틱 함수로는 맨해튼 거리와 유클리드 거리가 있습니다. 현재 노드의 좌표 $(x1, y1)$과 목표 노드 의 좌표 $(x2, y2)$에 대해 이러한 거리는 다음과 같이 계산 됩니다.
맨해튼 거리
\[\begin{flalign*} &h(n) = \left|x_1 - x_2\right| + \left|y_1 - y_2\right| & \end{flalign*}\]유클리드 거리
\[\begin{flalign*} &h(n) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} & \end{flalign*}\]총 예상 비용 $f(n)$
총 예상 비용(또는 평가 함수) $f(n)$은 A* 알고리즘 의사결정 과정의 초석으로, 실제 경로 비용과 각 노드의 잠재력을 평가하기 위한 휴리스틱 추정치를 모두 결합합니다. 앞서 설명하였듯 모든 노드 $n$에 대해 이 비용은 다음과 같이 계산됩니다.
\[\begin{flalign*} &f(n) = g(n) + h(n) & \end{flalign*}\]알고리즘은 이렇게 결합된 값을 사용하여 다음에 탐색할 노드를 전략적으로 선택하고, 항상 Open List에서 f(n) 값이 가장 낮은 노드를 선택하여 알려진 비용과 추정된 남은 거리 간의 최적의 균형을 보장합니다.
A* 의사코드
A*의 기본 구성을 이해했다면, 실제로 어떻게 작동하는지를 살펴봅시다.
알고리즘이 작동하는 방식은 다음과 같습니다.
vector<Node*> A_Star(Node* start, Node* goal) {
// open 리스트와 closed 리스트 초기화
vector<Node*> openList = { start }; // 평가할 노드 목록
vector<Node*> closedList; // 이미 평가된 노드 목록
// 시작 노드 초기화
start->g = 0; // 시작 노드까지의 비용은 0
start->h = heuristic(start, goal); // 휴리스틱 계산
start->f = start->g + start->h; // 총 예상 비용
start->parent = nullptr; // 경로 복원을 위한 포인터
while (!openList.empty()) {
// f 값이 가장 낮은 노드를 찾음
Node* current = getLowestFNode(openList);
// 목표 노드에 도달했는지 확인
if (current == goal) {
return reconstructPath(current);
}
// openList에서 제거하고 closedList에 추가
removeFromList(openList, current);
closedList.push_back(current);
// 모든 이웃 노드 확인
for (Node* neighbor : current->neighbors) {
if (contains(closedList, neighbor)) {
continue; // 이미 평가된 노드
}
// 임시 g 값 계산
double tentativeG = current->g + distance(current, neighbor);
// openList에 없다면 추가
if (!contains(openList, neighbor)) {
openList.push_back(neighbor);
}
// 이미 더 짧은 경로가 있다면 건너뜀
else if (tentativeG >= neighbor->g) {
continue;
}
// 더 나은 경로 발견 → 업데이트
neighbor->parent = current;
neighbor->g = tentativeG;
neighbor->h = heuristic(neighbor, goal);
neighbor->f = neighbor->g + neighbor->h;
}
}
return {}; // 경로를 찾을 수 없음
}
// 경로 복원 함수
vector<Node*> reconstructPath(Node* current) {
vector<Node*> path;
while (current != nullptr) {
path.insert(path.begin(), current); // 경로 맨 앞에 추가
current = current->parent;
}
return path;
}
의사코드를 풀어 설명하면 다음과 같습니다.
예시를 이해했다면 예시와 같은 말을 하고 있음을 알 수 있습니다.
초기화 단계
알고리즘을 시작하기 전에 전제되어야 하는 설정들입니다.
- Open List은 시작 노드로만 시작합니다.
- Close List은 비어 있는 상태로 시작됩니다.
각 노드는 4가지 중요한 정보를 저장합니다.
앞서 설명한 비용함수와 같은 내용입니다.
- $g$: 시작 노드의 실제 비용
- $h$: 목표 달성에 필요한 예상 비용
- $f$: $g$와 $h$의 합
- 부모: 이전 노드에 대한 참조(경로 재구성용)
Main loop
A*의 핵심은 다음 중 하나가 발생할 때까지 계속되는 메인 루프입니다.
- 목표 달성(성공)
- OpenList가 비어 있게 됩니다(실패 - 경로가 존재하지 않음)
각 반복 과정에서 알고리즘은 다음을 수행합니다.
- OpenList에서 가장 유망한 노드(가장 낮은 $f$ 값)를 선택합니다.
- CloseList으로 이동합니다.
- 모든 인접 노드를 조사합니다.
Neighbor evaluation
각 이웃 노드에 대해 이웃 평가 알고리즘은 다음과 같습니다.
- CloseList에 이미 있는 노드는 건너뜀
- 임시 $g$ 점수를 계산
- 더 나은 경로가 발견되면 노드 값을 업데이트
- OpenList에 새 노드를 추가
앞서 봤던 예시에서 1번 노드가 CloseList에 추가됨으로써 3번 노드의 상태값이 갱신되었던 부분이 해당 이웃 평가 알고리즘을 통해 동작한 것입니다.
그렇게 어렵지 않죠? 우리가 막연히 생각하는 로직을 정리했을 뿐입니다.
경로 재구성
해당 알고리즘은 목표에 도달하면(도착 노드가 CloseList에 추가되었다면) 부모 참조를 거꾸로 탐색하여 시작점에서 목표점까지 최적의 경로를 구성합니다.
유의할 점이라면 이정도가 될 것 같습니다.
- 휴리스틱 함수는 허용 가능합니다(과대평가 해서는 안됩니다..)
- 시작 노드와 목표 노드 사이에 실제로 경로가 존재해야 합니다.
C++ A* 구현
이제 이론과 의사코드를 이해했으니 C++으로 A*를 구현해 보겠습니다.
실제 구현을 구체화하기 위해 게임과 로봇 등에서 흔히 사용하는 2차원 그리드에 알고리즘을 구현해 보겠습니다.
2차원 그리드가 구현하기엔 비교적 쉽기도 합니다..ㅎ
먼저 필요한 라이브러리를 가져오고 검색 공간의 각 지점에 대한 위치 및 경로 정보를 저장할 노드 구조를 만듭니다.
#include <iostream>
#include <vector>
#include <queue>
#include <cmath>
#include <algorithm>
#include <functional>
using namespace std;
struct Node {
int x, y;
double g, h, f;
Node* parent;
Node(int x, int y)
: x(x), y(y), g(1e9), h(0), f(0), parent(nullptr) {}
};
// 4방향 이동
const int dx[] = { -1, 1, 0, 0 };
const int dy[] = { 0, 0, -1, 1 };
다음으로 경로 찾기 알고리즘을 지원하기 위해 몇 가지 보조 함수를 만들겠습니다.
- 맨해튼 거리를 사용하여 점 사이의 거리를 계산하는 함수
- 경계와 장애물을 면밀히 검토하여 그리드에서 유효한 이웃 위치를 찾는 함수
- 목표를 찾은 후 경로를 재구성하는 데 도움이 되는 함수 ..기타 부가적인 함수들을 만듭니다.
// 좌표 유효성 확인
bool inBounds(int x, int y, int rows, int cols) {
return 0 <= x && x < rows && 0 <= y && y < cols;
}
// 휴리스틱 함수 (맨해튼 거리)
double heuristic(Node* a, Node* b) {
return abs(a->x - b->x) + abs(a->y - b->y);
}
// 이동 비용 (가중치 없음)
double distance(Node* a, Node* b) {
return 1.0;
}
// 닫힌 목록 포함 여부
bool contains(const vector<Node*>& list, Node* node) {
return find(list.begin(), list.end(), node) != list.end();
}
// 경로 재구성
vector<Node*> reconstructPath(Node* current) {
vector<Node*> path;
while(current != nullptr) {
path.insert(path.begin(), current);
current = current->parent;
}
return path;
}
이제 핵심 알고리즘을 구현해 보겠습니다.
우선순위 큐를 사용하여 항상 가장 유망한 경로를 먼저 탐색하도록 구현하였습니다.
struct Compare {
bool operator()(const pair<double, Node*>& a, const pair<double, Node*>& b) const {
return a.first > b.first;
}
};
vector<Node*> A_Star(vector<vector<int>>& grid, Node* start, Node* goal, vector<vector<Node*>>& nodes) {
priority_queue<pair<double, Node*>, vector<pair<double, Node*>>, Compare> openQueue;
vector<Node*> closedList;
start->g = 0;
start->h = heuristic(start, goal);
start->f = start->g + start->h;
start->parent = nullptr;
openQueue.push({start->f, start});
while(!openQueue.empty()) {
Node* current = openQueue.top().second;
openQueue.pop();
if(current == goal) {
return reconstructPath(current);
}
if(contains(closedList, current)) {
continue;
}
closedList.push_back(current);
for(int dir = 0; dir < 4; ++dir) {
int nx = current->x + dx[dir];
int ny = current->y + dy[dir];
if(!inBounds(nx, ny, grid.size(), grid[0].size()) || grid[nx][ny] == 1) {
continue;
}
Node* neighbor = nodes[nx][ny];
double tentativeG = current->g + distance(current, neighbor);
if(tentativeG < neighbor->g) {
neighbor->parent = current;
neighbor->g = tentativeG;
neighbor->h = heuristic(neighbor, goal);
neighbor->f = neighbor->g + neighbor->h;
openQueue.push({neighbor->f, neighbor});
}
}
}
return {};
}
위 코드는 아직 탐색해야 하는 노드에 대한 열린 집합(=OpenList)과 이미 검사한 노드에 대한 닫힌 집합(=CloseList) 이 두가지 집합을 유지합니다. 우리는 격자를 탐색하면서 더 나은 경로를 찾을 때마다 경로 비용을 지속적으로 업데이트하여 목표에 도달할 때까지 계속합니다.
마지막으로 시각화 함수를 만들어 봅시다.
장애물이 있는 그리드 레이아웃을 보여주고, 계산된 최적 경로를 표시하도록 구성했습니다.
출력에서 장애물은 #으로, 장애물이 없다면 .으로, 계산된 최적 경로는 *으로 표시됩니다.
// 경로와 장애물 표시
void printGrid(vector<vector<int>>& grid, const vector<Node*>& path) {
for(Node* n : path) {
if(grid[n->x][n->y] == 0) {
grid[n->x][n->y] = 8;
}
}
for(int i = 0; i < grid.size(); ++i) {
for(int j = 0; j < grid[i].size(); ++j) {
if(grid[i][j] == 1) cout << "#";
else if(grid[i][j] == 8) cout << "*";
else cout << ".";
}
cout << '\n';
}
}
int main() {
int rows = 5, cols = 7;
vector<vector<int>> grid = {
{0, 0, 0, 0, 0, 0, 0},
{0, 1, 1, 1, 0, 1, 0},
{0, 0, 0, 1, 0, 1, 0},
{1, 1, 0, 0, 0, 0, 0},
{0, 0, 0, 1, 1, 1, 0},
};
vector<vector<Node*>> nodes(rows, vector<Node*>(cols));
for(int i = 0; i < rows; ++i)
for(int j = 0; j < cols; ++j)
nodes[i][j] = new Node(i, j);
Node* start = nodes[0][0];
Node* goal = nodes[4][6];
vector<Node*> path = A_Star(grid, start, goal, nodes);
printGrid(grid, path);
for(int i = 0; i < rows; ++i)
for(int j = 0; j < cols; ++j)
delete nodes[i][j];
return 0;
}
전체 코드는 다음과 같습니다.
#include <iostream>
#include <vector>
#include <queue>
#include <cmath>
#include <algorithm>
#include <functional>
using namespace std;
// 노드 구조체 정의
struct Node {
int x, y;
double g, h, f;
Node* parent;
Node(int x, int y)
: x(x), y(y), g(1e9), h(0), f(0), parent(nullptr) {}
};
// 4방향 이동
const int dx[] = { -1, 1, 0, 0 };
const int dy[] = { 0, 0, -1, 1 };
// 좌표 유효성 확인
bool inBounds(int x, int y, int rows, int cols) {
return 0 <= x && x < rows && 0 <= y && 0 <= y && y < cols;
}
// 휴리스틱 함수 (맨해튼 거리)
double heuristic(Node* a, Node* b) {
return abs(a->x - b->x) + abs(a->y - b->y);
}
// 이동 비용
double distance(Node* a, Node* b) {
return 1.0;
}
// 닫힌 목록에 포함되어 있는지 확인
bool contains(const vector<Node*>& list, Node* node) {
return find(list.begin(), list.end(), node) != list.end();
}
// 경로 재구성
vector<Node*> reconstructPath(Node* current) {
vector<Node*> path;
while (current != nullptr) {
path.insert(path.begin(), current);
current = current->parent;
}
return path;
}
// 우선순위 큐 비교자
struct Compare {
bool operator()(const pair<double, Node*>& a, const pair<double, Node*>& b) const {
return a.first > b.first;
}
};
// A* 알고리즘
vector<Node*> A_Star(vector<vector<int>>& grid, Node* start, Node* goal, vector<vector<Node*>>& nodes) {
priority_queue<pair<double, Node*>, vector<pair<double, Node*>>, Compare> openQueue;
vector<Node*> closedList;
start->g = 0;
start->h = heuristic(start, goal);
start->f = start->g + start->h;
start->parent = nullptr;
openQueue.push({ start->f, start });
while (!openQueue.empty()) {
Node* current = openQueue.top().second;
openQueue.pop();
if (current == goal) {
return reconstructPath(current);
}
if (contains(closedList, current)) {
continue;
}
closedList.push_back(current);
for (int dir = 0; dir < 4; ++dir) {
int nx = current->x + dx[dir];
int ny = current->y + dy[dir];
if (!inBounds(nx, ny, grid.size(), grid[0].size()) || grid[nx][ny] == 1) {
continue;
}
Node* neighbor = nodes[nx][ny];
double tentativeG = current->g + distance(current, neighbor);
if (tentativeG < neighbor->g) {
neighbor->parent = current;
neighbor->g = tentativeG;
neighbor->h = heuristic(neighbor, goal);
neighbor->f = neighbor->g + neighbor->h;
openQueue.push({ neighbor->f, neighbor });
}
}
}
return {};
}
// 경로 및 맵 시각화
void printGrid(vector<vector<int>>& grid, const vector<Node*>& path) {
for (Node* n : path) {
if (grid[n->x][n->y] == 0) {
grid[n->x][n->y] = 8;
}
}
for (int i = 0; i < grid.size(); ++i) {
for (int j = 0; j < grid[i].size(); ++j) {
if (grid[i][j] == 1) cout << "#";
else if (grid[i][j] == 8) cout << "*";
else cout << ".";
}
cout << '\n';
}
}
int main() {
int rows = 5, cols = 7;
vector<vector<int>> grid = {
{0, 0, 0, 0, 0, 0, 0},
{0, 1, 1, 1, 0, 1, 0},
{0, 0, 0, 1, 0, 1, 0},
{1, 1, 0, 0, 0, 0, 0},
{0, 0, 0, 1, 1, 1, 0},
};
vector<vector<Node*>> nodes(rows, vector<Node*>(cols));
for (int i = 0; i < rows; ++i)
for (int j = 0; j < cols; ++j)
nodes[i][j] = new Node(i, j);
Node* start = nodes[0][0];
Node* goal = nodes[4][6];
vector<Node*> path = A_Star(grid, start, goal, nodes);
printGrid(grid, path);
for (int i = 0; i < rows; ++i)
for (int j = 0; j < cols; ++j)
delete nodes[i][j];
return 0;
}
A* 알고리즘의 응용
A* 알고리즘은 최적의 경로 탐색 기능으로 인해 여러 분야에 널리 사용되고 있습니다.
간단하게만 살펴보고 넘어가겠습니다.
1. 게임 및 엔터테인먼트
가장 쉽게 생각해볼 수 있는 분야입니다. 캐릭터나 물체의 최적 경로를 구하는데에 사용한다면 활용 방법이 무궁무진 하겠네요.
- 전략 게임에서의 캐릭터 경로 찾기
- 오픈 월드 환경에서의 NPC 이동
- 전투 시나리오에서의 실시간 전술 계획
- 퍼즐 게임에서 미로 풀기
2. 내비게이션 시스템
경로 찾기 하면 역시 내비게이션을 빼놓을 수 없습니다.
A*는 거리와 잠재적 장애물 등 다양한 요소를 고려하여 경로를 최적화하는 내비게이션 시스템에서 널리 사용됩니다.
- GPS 애플리케이션에서의 경로 계획
- 교통 인식 내비게이션 서비스
- 대중교통 경로 최적화
- 실내 내비게이션 시스템
3. 로봇공학 및 자동화
여기서부터는 경로 찾기에 “최적화”를 중점적으로 활용한 분야입니다.
A* 알고리즘은 생산성과 안전을 위해 효율적인 움직임이 필수적인 로봇 공학에 필수적입니다.
- 자율 주행 차량 경로 계획
- 창고 로봇 탐색
- 드론 비행 경로 최적화
- 제조 로봇 이동 계획
4. 네트워크 시스템
이 역시 최적화를 중점적으로 생각한 경우입니다. A*는 리소스 활용과 라우팅의 효율성이 가장 중요한 네트워크 운영 최적화에도 적용됩니다.
- 네트워크 패킷 라우팅
- 분산 시스템에서의 리소스 할당
- 회로 기판 경로 설계
- 네트워크 케이블 라우팅 최적화
A*를 특히 가치 있게 만드는 것은 “최적화”가 비단 최단 거리에만 국한 되지 않는다는 점입니다. 사용자 정의 휴리스틱 함수를 통한 적응성으로, 거리, 시간, 에너지 사용량 등 다양한 지표에 대한 최적화를 가능하게 합니다.
마치며
A* 알고리즘은 경로 탐색 및 그래프 순회 문제에서(주로 경로 탐색에) 많이 사용됩니다.
A* 구현은 어려울 순 있지만, 잘 이해해 놓는다면 효율적인 솔루션을 만들 수 있을 겁니다.
제 글은 A*를 깊이 있게 이해하기 위해선 도움이 되기 어렵지만, A*가 어떤 알고리즘인지를 파악하는데에는 도움이 될 거라 생각합니다.
이 글이 A* 알고리즘을 이해하는데에 도움이 되었길 바라며, 글을 마칩니다.
부록 : 휴리스틱
앞서 A* 알고리즘의 비용 함수를 다룰 때, $h$ 함수에서 휴리스틱을 사용한 예상 경로를 구할 수 있었습니다.
A*는 휴리스틱 추정값을 사용하기 때문에, 해당 탐색 알고리즘이 다른 순회 방법과는 차별화되는 똑똑한 알고리즘이라고 할 수 있습니다.
휴리스틱은 간단하게 말해서 최적해를 찾기 위해 직관적 판단 또는 간단한 상식을 이용하는것입니다.
그리디 알고리즘도 이 휴리스틱 함수를 기반으로 사용되며, 이 휴리스틱 추정값을 어떤 방식으로 제공하느냐에
따라 얼마나 빨리 최단 경로를 파악할 수 있느냐가 결정됩니다.
가장 좋은 휴리스틱 함수는 문제의 구체적인 상황에 따라 달라지겠지만,
일반적으로 A* 알고리즘은 앞서 설명했듯 격자 기반 지도의 경우 맨해튼 거리, 개방 공간의 경우 유클리드 거리 등이 있습니다.

Comments