Trie 자료구조의 이해

9 minute read

Trie는 m-ary tree를 사용하여 문자열을 효율적으로 저장하고 검색할 수 있도록 설계된 트리 형태의 자료구조입니다.
접두사 트리(Prefix Tree)라고도 불리며, 문자열 검색, 자동완성, 사전 구현 등에 널리 사용됩니다.
해당 자료구조에 대해 간단히 다루어보겠습니다.

Trie

Trie 자료구조는 문자열의 집합을 트리 형태로 저장하는 자료구조입니다.
각 노드는 하나의 문자를 나타내며, 루트에서 특정 노드까지의 경로가 하나의 문자열을 형성하는 구조입니다.

왜 트라이를 사용할까요?
이는 전통적인 문자열 저장 방법들을 바라보면 알 수 있습니다.

배열/벡터 방식

 vector<string> dictionary = {"cat", "car", "card", "care", "careful"};

 // 검색 시간: O(n*m) - n개 문자열, 각각 평균 길이 m
 bool search(const vector<string>& dict, const string& word) {
     for (const string& s : dict) {
         if (s == word) return true;  // 문자열 비교: O(m)
     }
     return false;
 }

첫번째로 배열/벡터 방식을 바라봅시다.
특정 문자를 찾고자 하면 일반적으로 for문을 사용하여 찾을 수 있겠죠.
하지만 이 경우 검색시간은 $O(n*m)$ 입니다.
문자열 개수가 많아짐에 따라 검색 시간도 선형적으로 늘어납니다.

해시 테이블 방식
```
 unordered_set<string> hashDict = {"cat", "car", "card", "care", "careful"};

 // 검색 시간: 평균 O(m), 최악 O(n*m)
 // 접두사 검색 불가능
```
두번째로는 해시 테이블 방식을 떠올릴 수 있습니다.
하지만 이 또한 검색시간이 평균 $O(m)$, 최악 $O(n*m)$ 으로,
문자열 개수가 많아짐에 따라 검색 시간이 길어질 수 있습니다.

이러한 부분을 해소할 수 있는 자료구조가 Trie입니다.
Trie는 $O(m)$ 이라는 일정한 검색 시간을 가집니다.
저장된 문자열 개수와 무관하죠. 이는 굉장히 큰 메리트라고 볼 수 있습니다.

일반적인 해시 테이블이나 배열을 사용한 문자열 저장 방식과 비교했을 때,
공통 접두사를 공유하는 문자열들을 효율적으로 저장할 수 있다는 것이 특징입니다.

예시

다음 예시를 통해 살펴봅시다. “cat”, “car”, “card”, “care”, “careful”, “cars”, “do”, “dog”, “done” 문자열들을
Trie 자료구조에 저장하는 과정을 살펴보겠습니다.

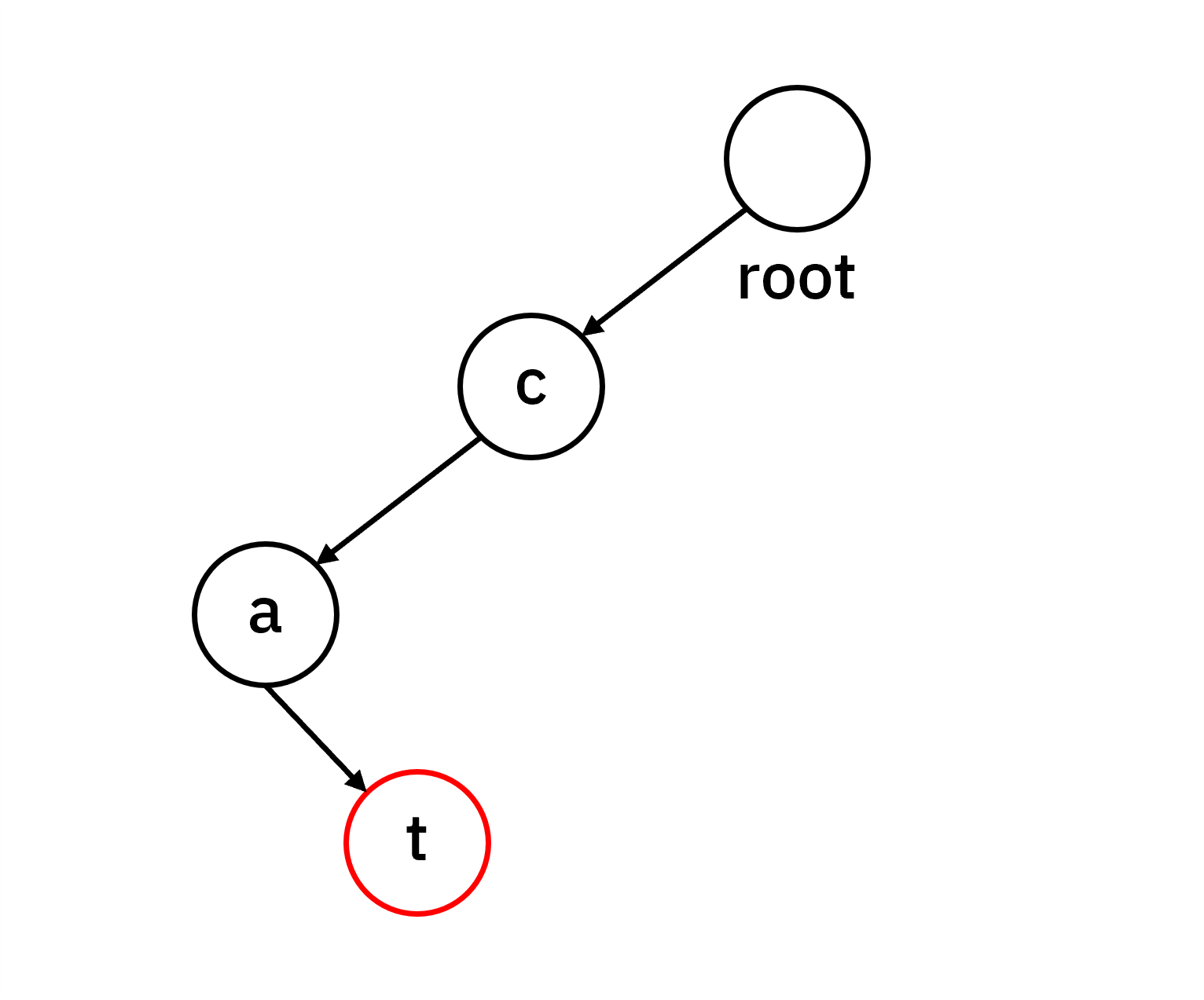
trie1

먼저 “cat”을 저장하는 과정입니다. 루트에서 시작하여 c → a → t 순으로 노드를 생성하고,
마지막 t 노드에 단어의 끝임을 표시합니다.
빨간색 테두리로 각 단어의 끝을 표시해놓겠습니다.

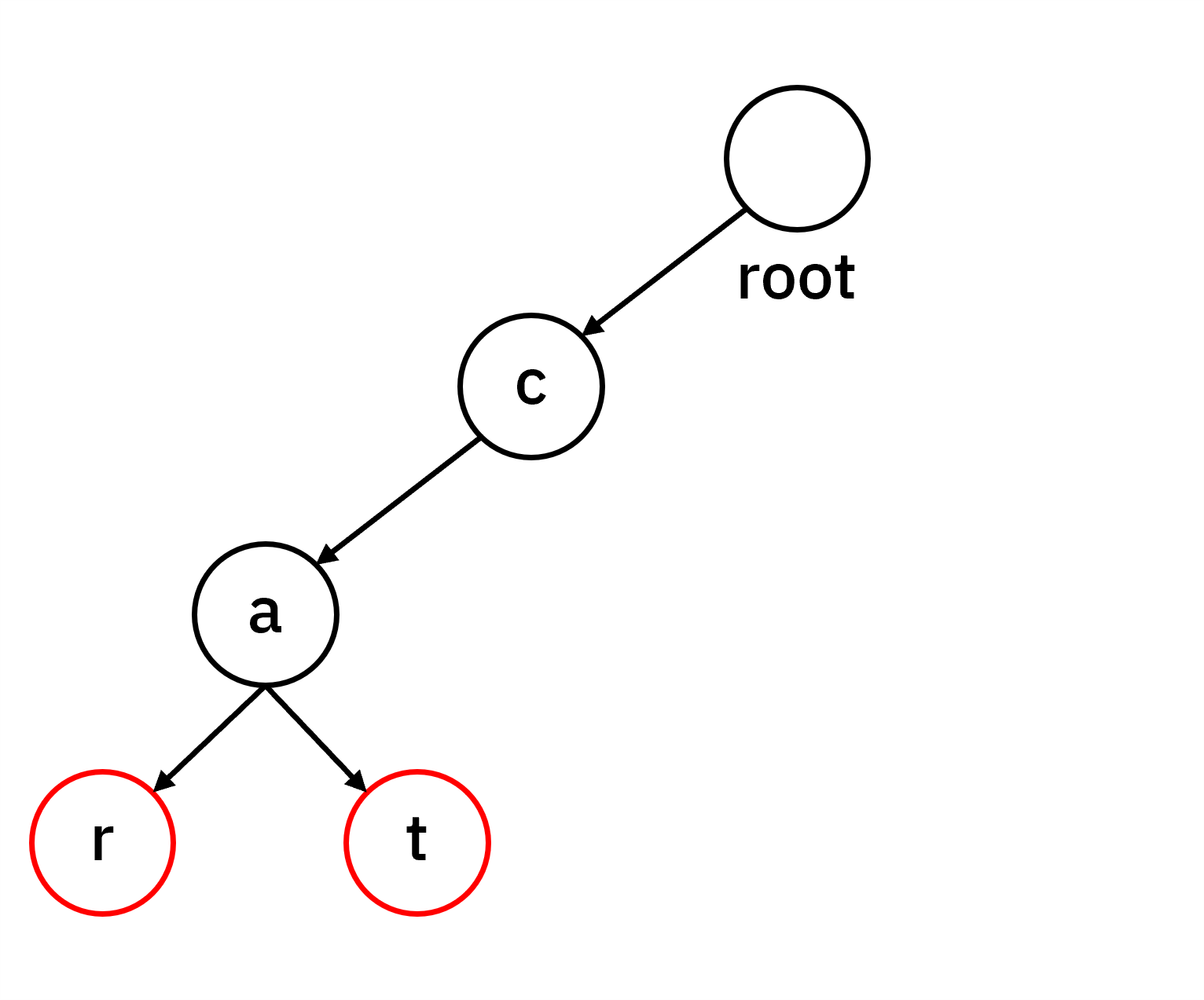
trie2

다음으로 “car”을 추가하면 “ca”까지는 기존 경로를 공유합니다. c → a까지는 동일한 경로를 사용하고, a 노드에서 새로운 r 노드를 생성합니다.

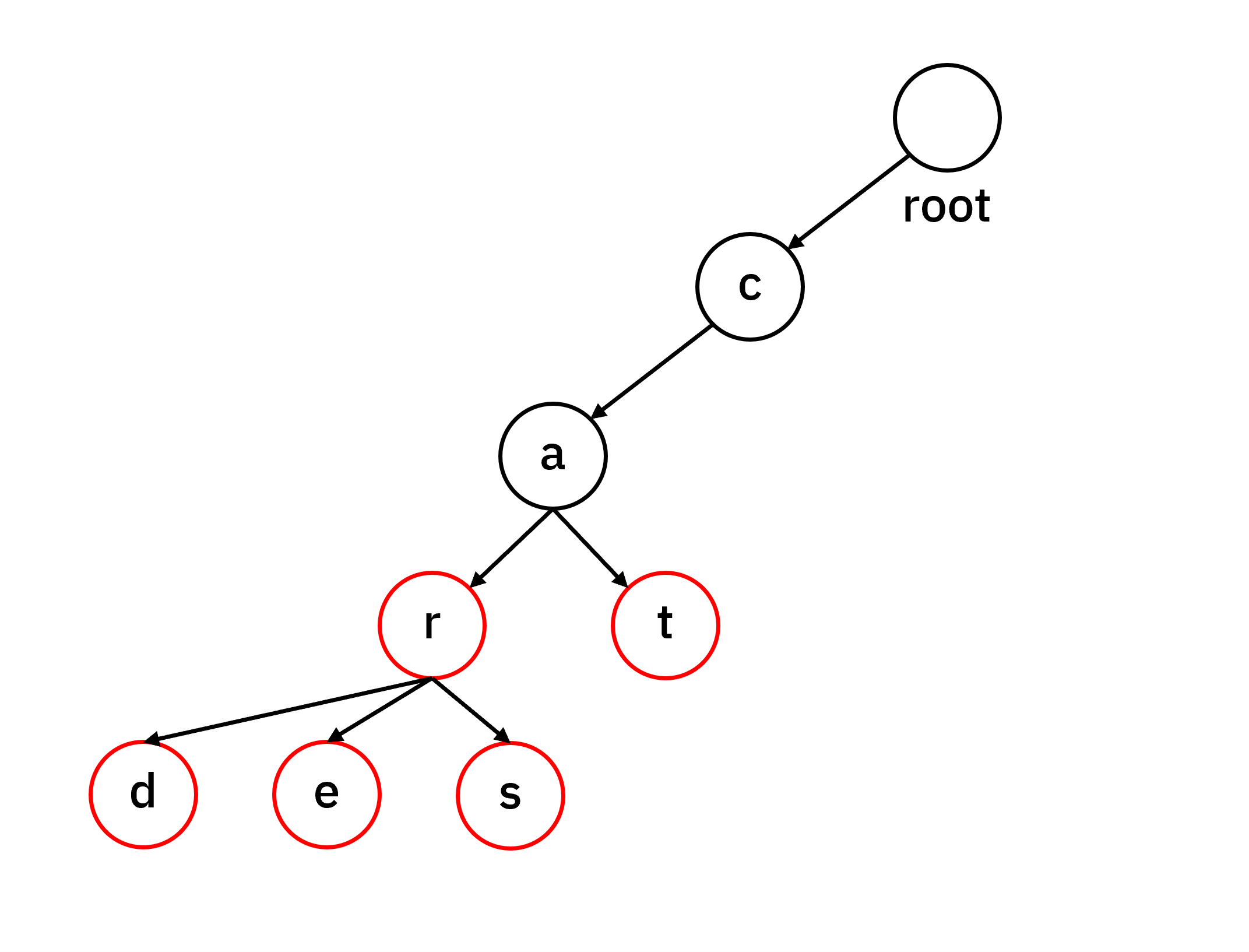
trie3

“card”와 “care”, “cars”를 추가하면서 조금 더 복잡한 구조가 형성됩니다.. “car” 경로를 공유한 후, r 노드에서 각각 d와 e, s로 분기됩니다.

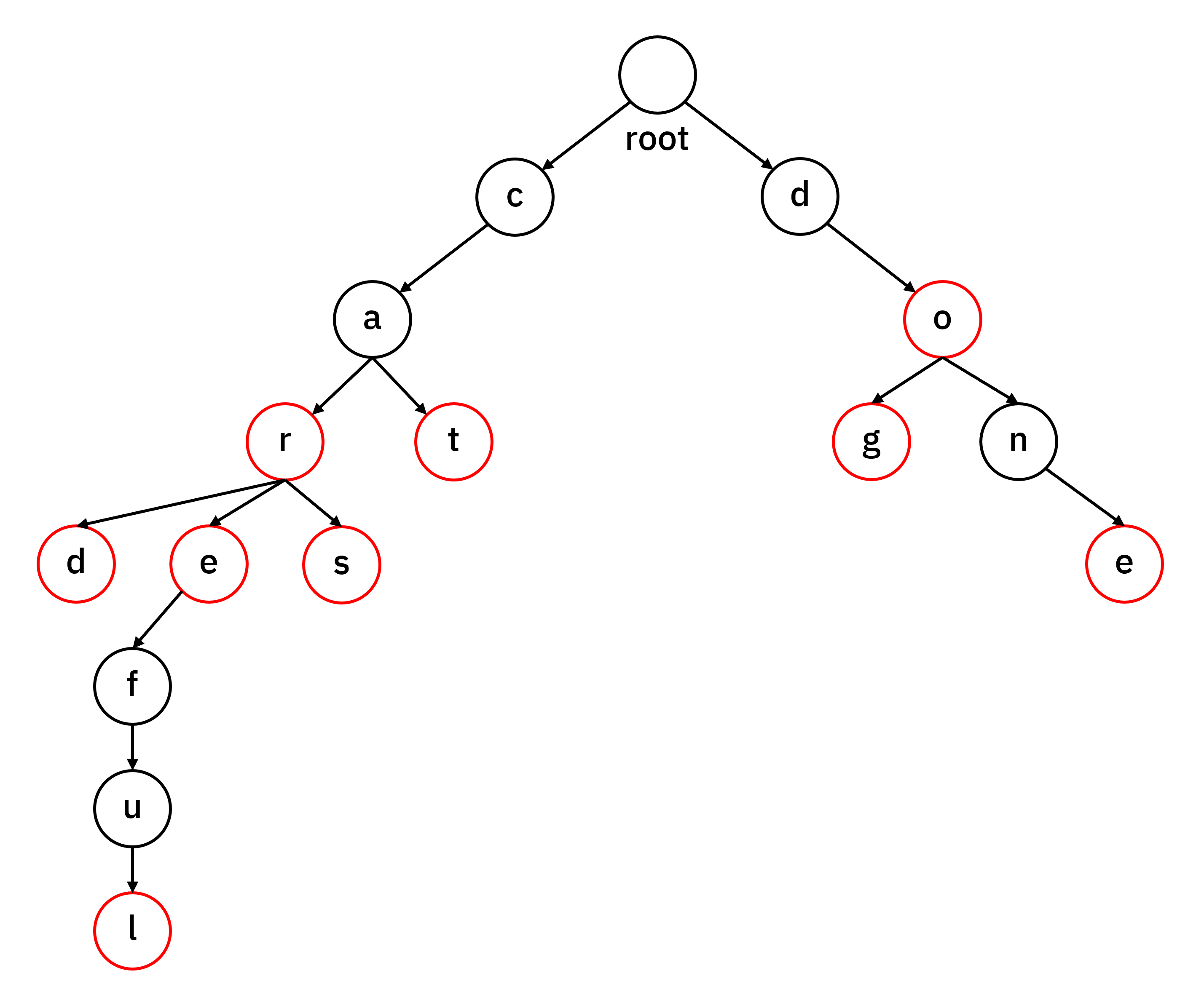
trie4

최종적으로 모든 문자열을 추가한 Trie는 위와 같은 형태가 됩니다. 공통 접두사를 가진 문자열들이 동일한 경로를 공유하여 메모리를 효율적으로 사용하는 것을 확인할 수 있습니다.

Trie 의사코드

Trie의 기본 구조와 주요 연산들의 의사코드를 살펴보겠습니다.

먼저 노드 구조를 살펴봅시다.

struct TrieNode {
    children: Map<Character, TrieNode>  // 자식 노드들
    isEndOfWord: Boolean                // 단어의 끝 여부
    
    constructor() {
        children = empty map
        isEndOfWord = false
    }
}

key를 해당 문자로, value를 자식 노드의 포인터로 받는 맵을 선언합니다.

만약 현재 노드에서 “cat”, “car” 단어가 시작된다면,
children[‘c’] → ‘c’로 시작하는 단어들을 처리하는 자식 노드
children[‘d’] → ‘d’로 시작하는 단어들을 처리하는 자식 노드
이런 식으로 저장이 됩니다.

isEndOfWord는 말 그대로 현재 노드가 완전한 단어의 끝인지를 표시하는 플래그입니다.
만약 “car”, “card”라는 단어가 있다면, r 노드에서도 완전한 단어가 될 수있으므로 이러한 플래그를 사용해야 합니다.

노드 구조를 만들었다면 삽입, 삭제, 검색 연산을 알아야겠죠?
먼저 삽입 연산을 살펴봅시다.

function insert(root, word):
    current = root
    
    for each character c in word:
        if c not in current.children:
            current.children[c] = new TrieNode()
        current = current.children[c]
    
    current.isEndOfWord = true

모든 단어는 루트에서 시작해서 아래쪽으로 내려가며 저장되기 때문에,
먼저 시작점을 설정(현재 위치를 루트 노드로 설정)합니다.

그리고 각 문자마다 자식 노드 존재 여부를 확인합니다.
예를 들어 “cat”라는 단어를 삽입하고자 하면,
현재 노드에서 문자 c로 가는 경로가 있는지 확인합니다.
조금 더 구체적으로 말하면, c문자로 가는 자식 노드가 있는지 확인하는 것입니다.

경로가 없는 경우, 새로운 노드를 생성하고 연결합니다.
이후 생성한 자식 노드로 이동합니다.

다음으로 검색 연산입니다.

function search(root, word):
    current = root
    
    for each character c in word:
        if c not in current.children:
            return false
        current = current.children[c]
    
    return current.isEndOfWord

앞서 선언해주었던 isEndOfWord 플래그를 활용 하여 특정 단어가 존재하는지 검색하는 연산입니다.

루트노드에서 검색을 시작하여 각 문자마다 경로가 존재하는지 확인하고 따라갑니다.
경로가 없다면 즉시 false를 반환하고 종료합니다.

하지만 경로가 모두 존재하더라도 해당 경로가 완전한 단어인지를 확인해야합니다.
따라서 isEndOfWord를 사용하여 완전한 단어인지에 대한 true/false를 반환하도록 합니다.

추가로, 접두사 검색 연산을 살펴보겠습니다.
해당 Trie에서 특정 접두사(prefix)로 시작하는 단어가 존재하는지 확인하는 연산입니다.

function startsWith(root, prefix):
    current = root
    
    for each character c in prefix:
        if c not in current.children:
            return false
        current = current.children[c]
    
    return true

검색 연산과 유사하나 차이점은 isEndOfWord를 사용하지 않고 무조건 true를 반환하는 것입니다.
완전한 단어가 아니더라도 true를 반환하도록 하여 접두사를 검색할 수 있는 것이죠.
말이 거창할 뿐이지 검색 연산의 함수와 비교했을 때 반환값 하나 바꾼게 다입니다.

이제 삭제 연산을 살펴봅시다.
삭제 연산은 다른 단어에 영향을 주지 않으면서 불필요한 노드들까지 정리해야하는 로직이기 때문에, 조금은 복잡한 코드를 가집니다.

function delete(root, word):
    return deleteHelper(root, word, 0)
    
function deleteHelper(node, word, depth):
    if node is null:
        return false
    
    if depth == word.length:
        if not node.isEndOfWord:
            return false
        node.isEndOfWord = false
        return node.children.isEmpty()
    
    char = word[depth]
    childNode = node.children[char]
    shouldDeleteChild = deleteHelper(childNode, word, depth + 1)
    
    if shouldDeleteChild:
        delete childNode
        node.children.remove(char)
        return not node.isEndOfWord and node.children.isEmpty()
    
    return false

위 코드는 재귀적으로 단어를 찾아가면서 삭제하는 deleteHelper 함수를 핵심으로 사용합니다.
길이가 비교적 긴 편이니 나누어 보겠습니다.

    if node is null:
        return false

잘못된 경로로 진입했거나 단어가 존재하지 않는다면 false를 반환합니다.

if depth == word.length:
        if not node.isEndOfWord:
            return false
        node.isEndOfWord = false
        return node.children.isEmpty()

해당 위치에서 완전한 단어가 불가능한 경우 삭제할 수 없으므로 false를 반환하고,
아니라면 우선 플래그 값을 false로 설정합니다. 단어의 끝이라는 마킹을 제거한다고 보시면 됩니다.

그리고나서 해당 노드에서 자식 노드 존재 여부에 따라 삭제 가능 여부를 반환합니다.

    char = word[depth]
    childNode = node.children[char]
    shouldDeleteChild = deleteHelper(childNode, word, depth + 1)

현재 깊이의 문자를 추출하여 해당 문자의 자식 노드를 통해 재귀적으로 더 깊이 들어갑니다.

    if shouldDeleteChild:
        delete childNode
        node.children.remove(char)
        return not node.isEndOfWord and node.children.isEmpty()

shouldDeleteChild는 방금 본 재귀적 호출 구문에서 반환값을 받는 친구입니다.
이 부분은 삭제연산 함수의 마지막 부분이고, 여기서 true값을 반환받는다면 조건을 만족합니다.
return 값을 바라보면 해당 노드가 완전한 단어가 가능한 지점이면서 자식 노드가 없어야 하는 마지막 노드인 경우 true를 반환하도록 하고 있습니다.

…쉽게 말해서 자식 노드가 없는 노드라면 삭제하는 과정입니다.

다른 단어에 영향을 주지 않아야 하기 때문에 이러한 번거로운 과정을 거칩니다.

C++ Trie 구현

의사코드를 바탕으로 Trie를 C++로 구현한 코드입니다.

#include <iostream>
#include <unordered_map>
#include <string>
#include <vector>
using namespace std;

struct TrieNode {
    unordered_map<char, TrieNode*> children;
    bool isEnd;
    
    TrieNode() : isEnd(false) {}
};

class Trie {
private:
    TrieNode* root;
    
public:
    Trie() {
        root = new TrieNode();
    }
    
    void insert(const string& word) {
        TrieNode* cur = root;
        for (char c : word) {
            if (!cur->children[c]) {
                cur->children[c] = new TrieNode();
            }
            cur = cur->children[c];
        }
        cur->isEnd = true;
    }
    
    bool search(const string& word) {
        TrieNode* cur = root;
        for (char c : word) {
            if (!cur->children[c]) {
                return false;
            }
            cur = cur->children[c];
        }
        return cur->isEnd;
    }
    
    bool startsWith(const string& prefix) {
        TrieNode* cur = root;
        for (char c : prefix) {
            if (!cur->children[c]) {
                return false;
            }
            cur = cur->children[c];
        }
        return true;
    }
    
    void getAllWords(TrieNode* node, string& current, vector<string>& result) {
        if (node->isEnd) {
            result.push_back(current);
        }
        for (auto& p : node->children) {
            current.push_back(p.first);
            getAllWords(p.second, current, result);
            current.pop_back();
        }
    }
    
    vector<string> getWordsWithPrefix(const string& prefix) {
        TrieNode* cur = root;
        for (char c : prefix) {
            if (!cur->children[c]) {
                return {};
            }
            cur = cur->children[c];
        }
        
        vector<string> result;
        string current = prefix;
        getAllWords(cur, current, result);
        return result;
    }
};

int main() {
    Trie trie;
    
    vector<string> words = {"cat", "car", "card", "care", "careful", "dog", "dodge"};
    for (const string& word : words) {
        trie.insert(word);
    }
    
    cout << trie.search("car") << "\n";
    cout << trie.startsWith("ca") << "\n";
    
    vector<string> prefixWords = trie.getWordsWithPrefix("car");
    for (const string& word : prefixWords) {
        cout << word << " ";
    }
    cout << "\n";
    
    return 0;
}

Trie의 최적화

장점이 있으면 단점도 있겠죠. Trie의 단점하면 가장 먼저 꼽히는 것은 필요한 메모리가 너무 크다는 것입니다.
기본적인 Trie 구현은 메모리 사용량이 클 수 있습니다.

하지만 우리는 압축 Trie를 사용하여 이 단점을 약간이나마 개선할 수 있습니다. 압축 Trie에 대해 간단하게 알아보겠습니다.

압축 Trie

압축 Trie(Compressed Trie 또는 Radix Tree)는 메모리 사용량을 줄이기 위해
연속된 단일 경로를 하나의 노드로 압축한 Trie입니다.

자식이 하나뿐인 노드를 부모 노드와 합치는 방식으로 공간과 시간복잡도를 개선한 방식입니다.
말 그대로 압축…입니다.

“cat”, “car”, “card” 라는 단어를 기존 Trie 방식으로 저장하면 다음과 같습니다.

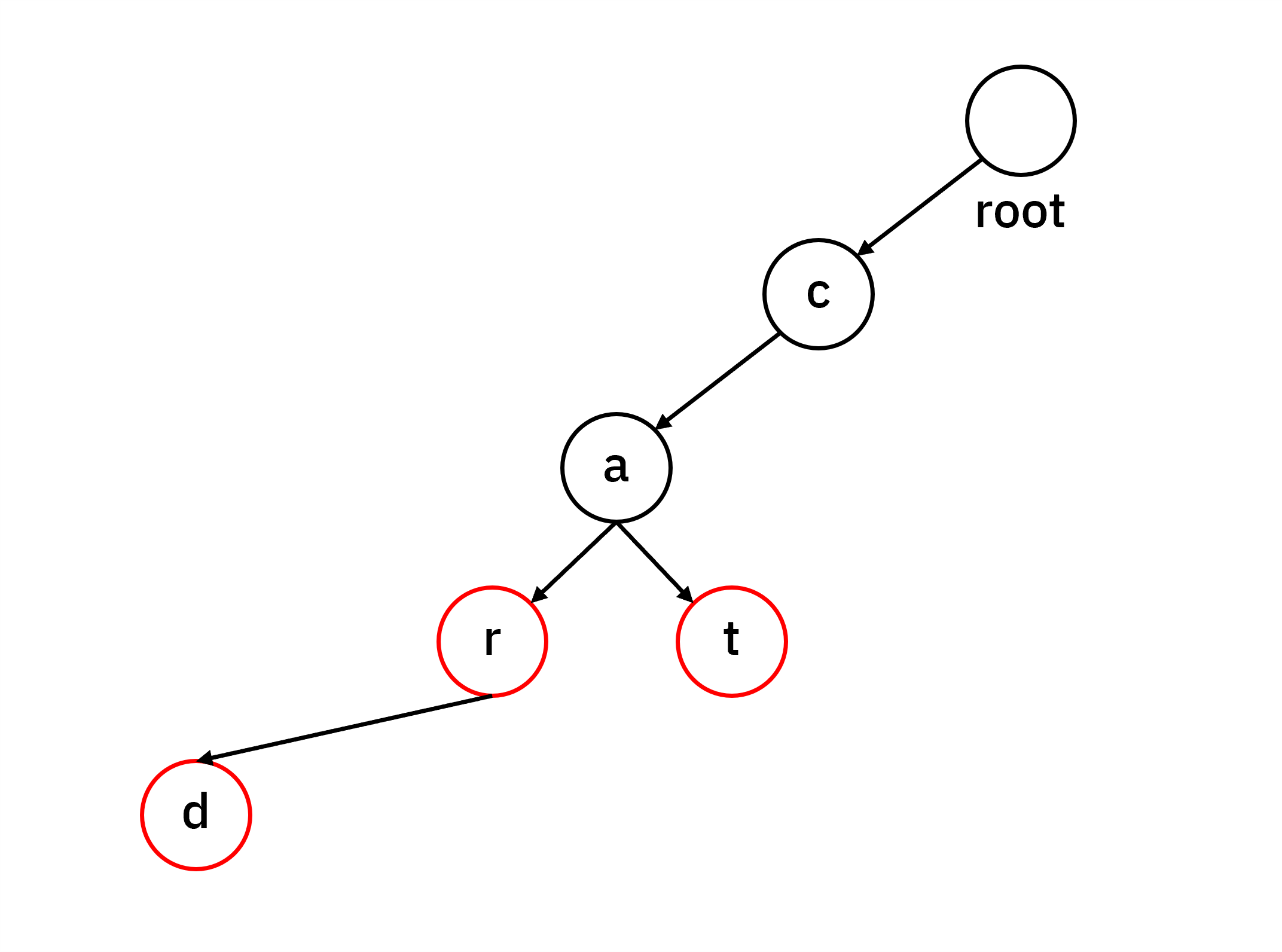
trie5

이를 압축 Trie로 저장하면 다음과 같습니다.

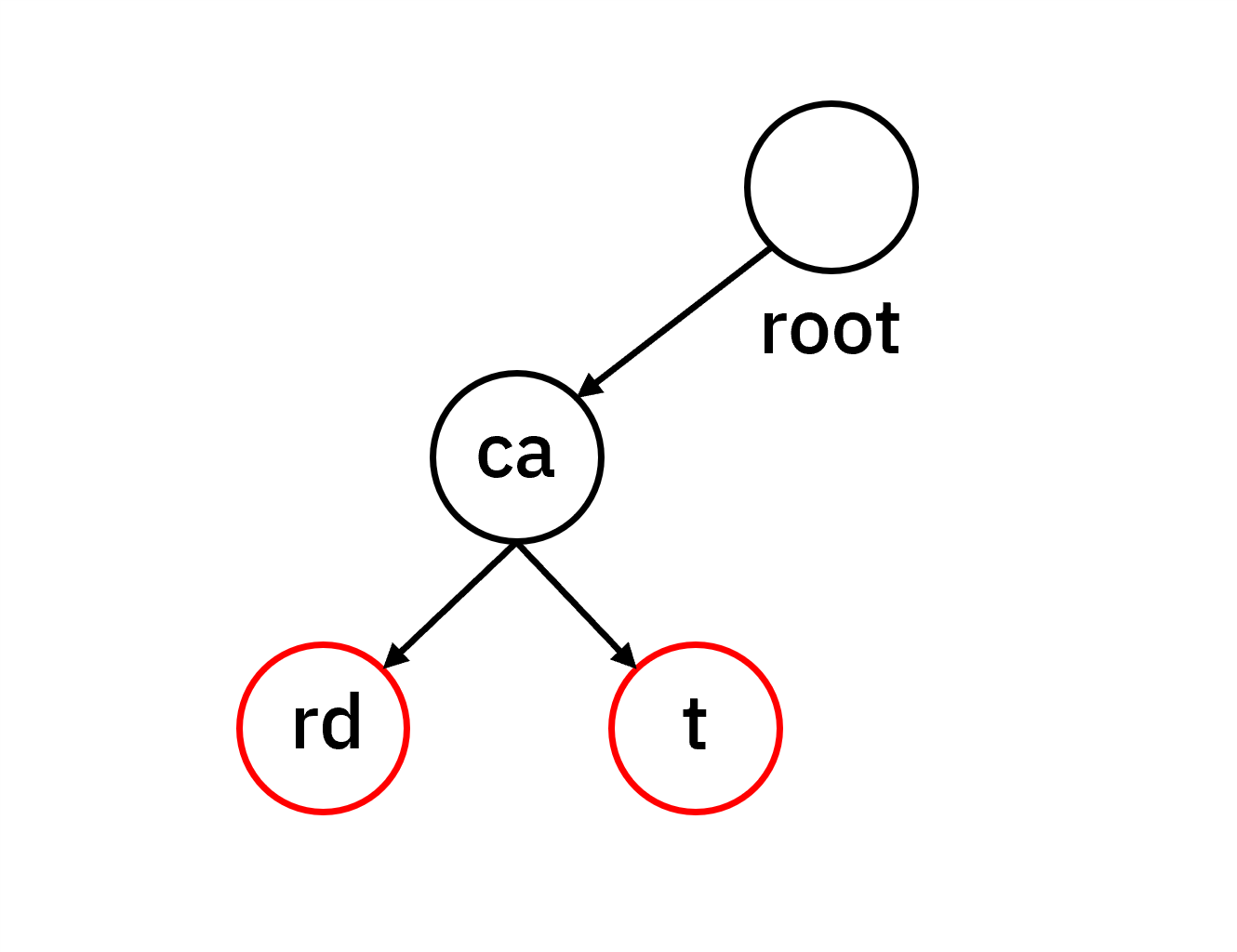
compressed_trie

이를 C++로 구현한 코드입니다.

#include <iostream>
#include <unordered_map>
#include <string>
#include <vector>
using namespace std;

struct CompressedTrieNode {
    unordered_map<char, CompressedTrieNode*> children;
    string edge;
    bool isEnd;
    
    CompressedTrieNode() : isEnd(false) {}
    CompressedTrieNode(string str) : edge(str), isEnd(false) {}
};

class CompressedTrie {
private:
    CompressedTrieNode* root;
    
    int commonPrefixLength(const string& str1, const string& str2) {
        int len = min(str1.length(), str2.length());
        int i = 0;
        while (i < len && str1[i] == str2[i]) {
            i++;
        }
        return i;
    }
    
    void splitNode(CompressedTrieNode* node, int splitPos) {
        string restEdge = node->edge.substr(splitPos);
        node->edge = node->edge.substr(0, splitPos);
        
        CompressedTrieNode* newChild = new CompressedTrieNode(restEdge);
        newChild->isEnd = node->isEnd;
        newChild->children = node->children;
        
        node->children.clear();
        node->isEnd = false;
        node->children[restEdge[0]] = newChild;
    }
    
public:
    CompressedTrie() {
        root = new CompressedTrieNode();
    }
    
    void insert(const string& word) {
        CompressedTrieNode* cur = root;
        int wordPos = 0;
        
        while (wordPos < word.length()) {
            char firstChar = word[wordPos];
            
            if (!cur->children[firstChar]) {
                string remainingWord = word.substr(wordPos);
                cur->children[firstChar] = new CompressedTrieNode(remainingWord);
                cur->children[firstChar]->isEnd = true;
                return;
            }
            
            CompressedTrieNode* child = cur->children[firstChar];
            string remainingWord = word.substr(wordPos);
            int commonLen = commonPrefixLength(child->edge, remainingWord);
            
            if (commonLen == child->edge.length()) {
                cur = child;
                wordPos += commonLen;
            } else {
                splitNode(child, commonLen);
                
                if (commonLen == remainingWord.length()) {
                    child->isEnd = true;
                    return;
                } else {
                    string newEdge = remainingWord.substr(commonLen);
                    child->children[newEdge[0]] = new CompressedTrieNode(newEdge);
                    child->children[newEdge[0]]->isEnd = true;
                    return;
                }
            }
        }
        
        cur->isEnd = true;
    }
    
    bool search(const string& word) {
        CompressedTrieNode* cur = root;
        int wordPos = 0;
        
        while (wordPos < word.length()) {
            char firstChar = word[wordPos];
            
            if (!cur->children[firstChar]) {
                return false;
            }
            
            CompressedTrieNode* child = cur->children[firstChar];
            string remainingWord = word.substr(wordPos);
            
            if (child->edge.length() > remainingWord.length()) {
                return false;
            }
            
            if (remainingWord.substr(0, child->edge.length()) != child->edge) {
                return false;
            }
            
            wordPos += child->edge.length();
            cur = child;
        }
        
        return cur->isEnd;
    }
    
    bool startsWith(const string& prefix) {
        CompressedTrieNode* cur = root;
        int prefixPos = 0;
        
        while (prefixPos < prefix.length()) {
            char firstChar = prefix[prefixPos];
            
            if (!cur->children[firstChar]) {
                return false;
            }
            
            CompressedTrieNode* child = cur->children[firstChar];
            string remainingPrefix = prefix.substr(prefixPos);
            int commonLen = commonPrefixLength(child->edge, remainingPrefix);
            
            if (commonLen < min(child->edge.length(), remainingPrefix.length())) {
                return false;
            }
            
            prefixPos += commonLen;
            cur = child;
            
            if (commonLen == remainingPrefix.length()) {
                return true;
            }
        }
        
        return true;
    }
    
    void printTrie(CompressedTrieNode* node, int depth = 0) {
        if (!node) return;
        
        for (int i = 0; i < depth; i++) cout << "  ";
        cout << "\"" << node->edge << "\"";
        if (node->isEnd) cout << " (END)";
        cout << "\n";
        
        for (auto& p : node->children) {
            printTrie(p.second, depth + 1);
        }
    }
    
    void print() {
        cout << "Compressed Trie structure:\n";
        printTrie(root);
    }
};

int main() {
    CompressedTrie ctrie;
    
    vector<string> words = {"cat", "car", "card"};
    
    cout << "Inserting words: ";
    for (const string& word : words) {
        cout << word << " ";
        ctrie.insert(word);
    }
    cout << "\n\n";
    
    ctrie.print();
    cout << "\n";
    
    cout << "Search results:\n";
    vector<string> testWords = {"cat", "car", "card", "ca", "care"};
    for (const string& word : testWords) {
        cout << "search(\"" << word << "\"): " << ctrie.search(word) << "\n";
    }
    
    cout << "\nPrefix search results:\n";
    vector<string> testPrefixes = {"ca", "car", "cat", "x"};
    for (const string& prefix : testPrefixes) {
        cout << "startsWith(\"" << prefix << "\"): " << ctrie.startsWith(prefix) << "\n";
    }
    
    return 0;
}

마치며

Trie 자료구조는 문자열 처리에 특화된 효율적인 자료구조입니다. 기본 Trie부터 Aho-Corasick, 압축 Trie까지 다양한 변형이 존재하니 여러 자료를 찾아보는걸 추천드립니다. Aho-Corasick도 같이 다루어보려고 했으나 분량이 너무 길어서 이후 따로 다루어 보겠습니다.

auto_search

검색 엔진의 자동완성, 사전 애플리케이션, 텍스트 에디터의 단어 완성 기능 등 우리가 일상적으로 사용하는 많은 애플리케이션에서 Trie가 활용되고 있습니다. 앞서 말했듯 메모리 사용량과 구현 복잡도를 고려하여 적절한 변형을 선택하는 것이 중요합니다.

이 글이 Trie 자료구조를 이해하는데에 도움이 되었길 바라며, 글을 마칩니다.

byte348

Trie 자료구조의 이해

Trie

예시

Trie 의사코드

C++ Trie 구현

Trie의 최적화

압축 Trie

마치며

Comments

You May Also Enjoy

A* 알고리즘의 이해

baekjoon 7869. 두 원

baekjoon 16192. Voronoi Diagram Returns

baekjoon 14940. 쉬운 최단거리