baekjoon 2987. 사과나무
문제 출처
Croatian Open Competition in Informatics > COCI 2007/2008 > Contest #5 3번
풀이
땅의 넓이는 문제에서 알려준 삼각형의 넓이 공식을 이용해서 구할 수 있습니다.
\[\begin{flalign*} &\frac{\left| x_A (y_B - y_C) + x_B (y_C - y_A) + x_C (y_A - y_B) \right|}{2} & \end{flalign*}\]문제는 소유한 사과나무의 개수를 구하는 것인데, 이는 삼각형 내부의 한 점에서 각 꼭짓점을 연결해 생기는 세 작은 삼각형의 넓이 합이 원래 삼각형의 넓이와 같다는 성질을 이용해서 풀 수 있습니다.
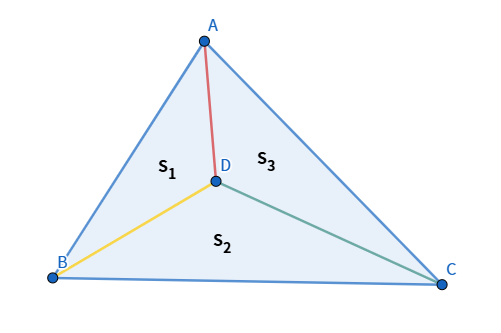
따라서 만약 점 $D$가 $S_{total} = S_1 + S_2 + S_3$ 를 만족시키면 점 $D$는 삼각형 내부의 점입니다.
사과나무의 개수를 조금 더 어렵게 구하는 방법이 있는데, 바로 볼록 다각형 내부의 점(Point in convex polygon) 판정 방식을 이용하는 방법입니다.
우선 볼록 다각형이란, 내각이 180°가 넘지 않는 단순한 다각형을 말합니다.
볼록하지 않은 다각형은 오목 다각형이라고 합니다.
볼록 다각형 내부의 점 판정 방식은 외적을 이용한 방향 판정을 사용합니다.
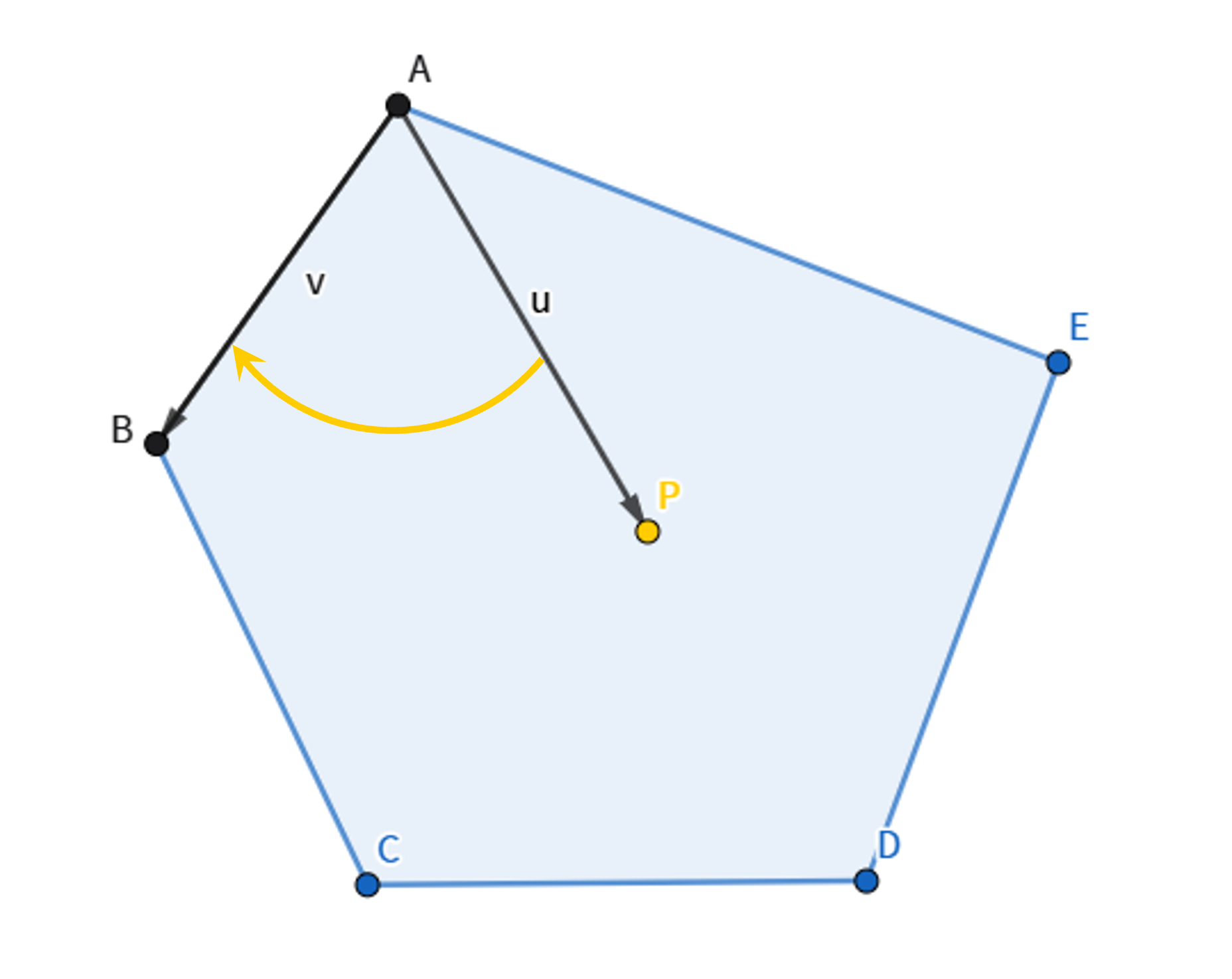
두 벡터 $\vec{u}$ 와 $\vec{v}$ 에 대해
$ \vec{u} × \vec{v} = u_x v_y - u_y v_x $ 이고
이 결과값이 양수라면 반시계 방향, 음수라면 시계 방향, 0이라면 두 벡터가 같은 직선 위에 있다는 상대적인 방향 판별이 가능합니다.
이렇게 두 벡터의 방향성을 판단하는 방법을 CCW(Counter-ClockWise, 반시계 방향)라고 하며, 기초적인 기하학 개념으로서 다각형 내부의 점 판정이나 선분 교차 검사 등에 사용합니다.
볼록 다각형의 꼭짓점은 내각이 180°를 넘지 않기 때문에, 내부의 점과 다각형의 각 변을 이루는 두 꼭짓점으로 만든 벡터들의 외적 부호가 모두 동일합니다. 이 성질을 이용하여, 판정하려는 점과 모든 변에 대해 외적을 계산했을 때 그 부호가 모두 같으면 해당 점은 다각형 내부에 있다고 판단할 수 있습니다. 아래 그림에서 점 $P$와 모든 변에 대해 외적을 계산했을 때 모두 같은 부호를 가지므로(각 벡터쌍의 상대적 방향 = 반시계 방향) 점 $P$는 다각형 내부에 있음을 증명할 수 있습니다.
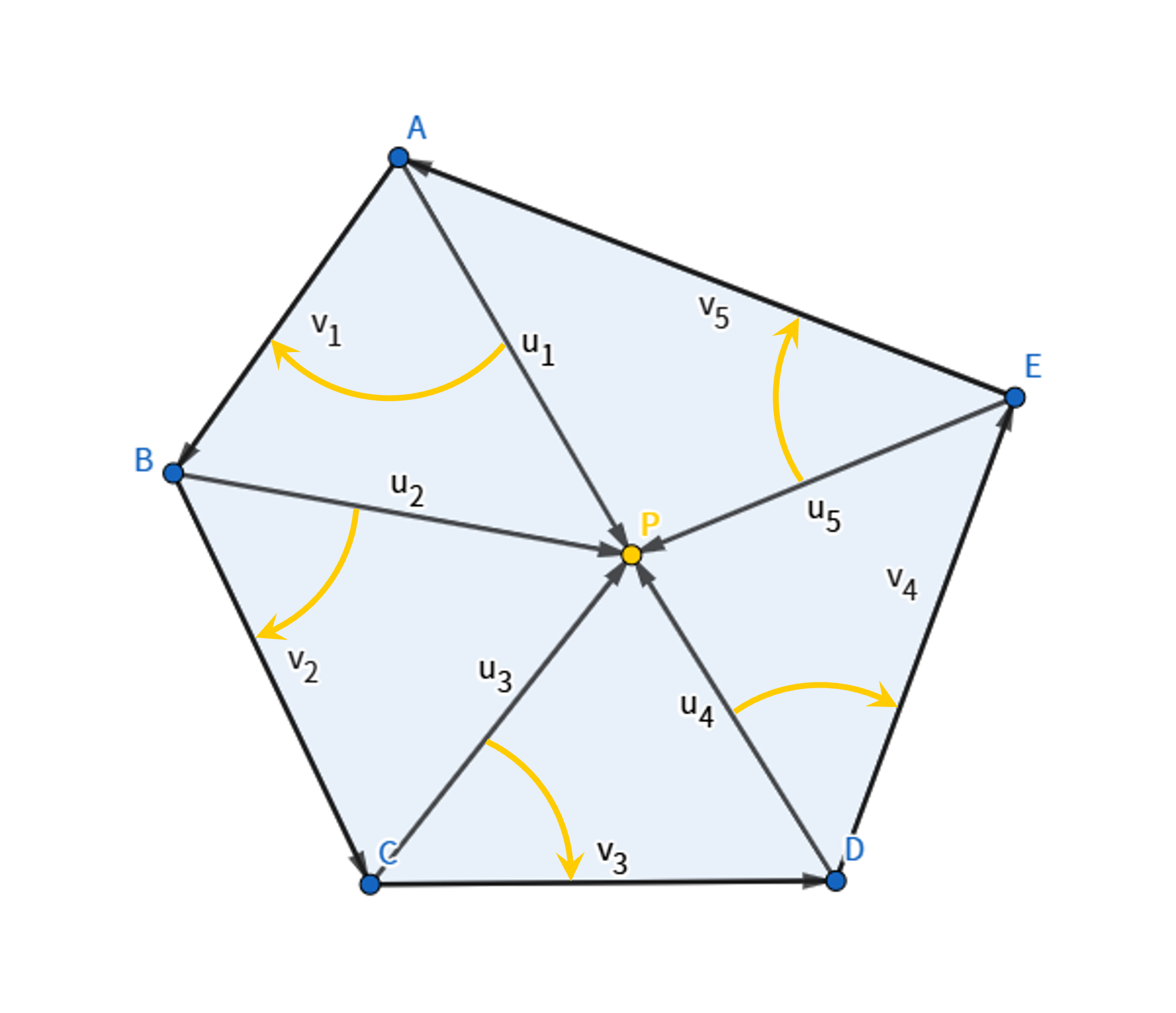
만약 어느 한 변에서 외적 부호가 달라진다면 그 점은 다각형 외부에 위치하게 됩니다.
따라서, 사과나무가 있는 좌표가 주어졌을 때, 볼록 다각형 내부 판정을 통해 해당 점들이 삼각형 안에 포함되는지를 정확하게 판별할 수 있습니다.
전체 코드
삼각형 성질을 이용한 풀이
#include <iostream>
#include <vector>
#include <cmath>
#include <iomanip>
using namespace std;
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
int xA, yA, xB, yB, xC, yC;
cin >> xA >> yA >> xB >> yB >> xC >> yC;
double S = abs(xA*(yB-yC) + xB*(yC-yA) + xC*(yA-yB)) / 2.0;
int N, x, y, count = 0;
cin >> N;
for(int i = 0; i < N; i++) {
cin >> x >> y;
double s1 = abs(x*(yB-yC) + xB*(yC-y) + xC*(y-yB)) / 2.0;
double s2 = abs(xA*(y-yC) + x*(yC-yA) + xC*(yA-y)) / 2.0;
double s3 = abs(xA*(yB-y) + xB*(y-yA) + x*(yA-yB)) / 2.0;
if(s1+s2+s3 == S) count++;
}
cout << fixed << setprecision(1) << S << '\n' << count << '\n';
return 0;
}
볼록 다각형 내부의 점 판정을 이용한 풀이
(문제에서 다각형은 삼각형으로 고정되어 있기 때문에 조금 하드하게 코딩했습니다.)
#include <iostream>
#include <cmath>
#include <iomanip>
using namespace std;
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
int xA, yA, xB, yB, xC, yC;
cin >> xA >> yA >> xB >> yB >> xC >> yC;
int ux = xB-xA, uy = yB-yA;
int vx = xC-xA, vy = yC-yA;
double S = abs(ux*vy - uy*vx) / 2.0;
int N, count = 0;
cin >> N;
for(int i = 0; i < N; i++) {
int xP, yP;
cin >> xP >> yP;
int ABx = xB-xA, ABy = yB-yA;
int APx = xP-xA, APy = yP-yA;
int c1 = ABx*APy - ABy*APx;
int BCx = xC-xB, BCy = yC-yB;
int BPx = xP-xB, BPy = yP-yB;
int c2 = BCx*BPy - BCy*BPx;
int CAx = xA-xC, CAy = yA-yC;
int CPx = xP-xC, CPy = yP-yC;
int c3 = CAx*CPy - CAy*CPx;
if((c1 >= 0 && c2 >= 0 && c3 >= 0) || (c1 <= 0 && c2 <= 0 && c3 <= 0)) count++;
}
cout << fixed << setprecision(1) << S << '\n' << count << '\n';
return 0;
}

Comments